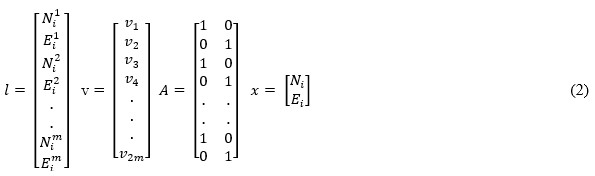Article of the Month - November 2020
|
A method to estimate a best fit trajectory from
multiple individual trajectories
This article in .pdf-format
(17 pages)

Ola Øvstedal, Norway
SUMMARY
In applications like extracting hiking trials from crowd sourced
data, collecting trajectories describing animal movement or precise
mapping of road lines, there are multiple trajectories, obtained from
e.g. Global Navigation Satellite Systems (GNSS), that describe the same
physical path. Due to e.g. observation techniques, occasional
observational blunders and difficulty in identifying exactly the same
physical path, individual trajectories will normally differ from one
another. This paper proposes a method on how to estimate a best fit
trajectory based on available individual trajectories. The precision of
the estimated trajectory is quantified in form of standard deviations.
Occasional observational blunders and failure in following the same
physical path are addressed through statistical testing. A priori
stochastic information regarding the individual trajectories is utilized
in a weighting scheme. The proposed method is first verified using a
simulated dataset. Results from processing of a relatively complex
dataset stemming from individual runs with a GPS multi-sport watch,
point out some advantages and drawbacks of the method. The method
appears to handle well both observational blunders and changing
requirements regarding following the very same physical path during data
collection. Detection and subsequent deletion of erroneous observations
might however introduce small jumps along the estimated trajectory.
Depending on the applications, the effect of occasional small jumps can
be handled by post smoothing.
1. INTRODUCTION
GNSS (Global Navigation Satellite Systems) like GPS (Global
Positioning System) is frequently used in kinematic mode to obtain
trajectories in the form of temporally ordered sequences of geographic
coordinates. Depending on factors like hardware, software, observation-
and processing techniques, satellite geometry and observational errors
from e.g. atmosphere and multipath (e.g. Teunissen & Montenbruck, 2017)
positional accuracies ranging from centimeter to several tens of meters
can be achieved.
Precise georeferencing of centerlines of roads is an example where a
high accuracy is required while an accuracy of a few meters is
sufficient for e.g. hiking trials. Most users require that quality
numbers should accompany the coordinates, e.g. standard deviations or
Dilution of Precision (DOP). If a trajectory is measured only once,
statistical information from the GNSS-processing can supply such quality
information. As with nearly all measuring techniques however,
observational blunders in the form of outliers will occasionally lead to
erroneous coordinates. An approach to overcome and reduce the effect of
outliers is to repeat the measurements leading to a redundant set of
trajectories. The problem then arises on how to estimate an optimal
trajectory based on individually measured trajectories as well as how to
compute corresponding quality numbers.
Each trajectory will not have identical sampling
locations as common tie points are normally not available. Each
trajectory is obtained individually and differences regarding start and
stop of each trajectory, epoch interval, speed and occasionally missing
epochs make the estimation of an optimal trajectory complicated.
Existing methods like manual methods, Mean and Median methods (Buchim
et al., 2013) and Dynamic Time Warping (Vaughan & Gabrys, 2016) have
different strengths and weaknesses regarding different sampling
characteristics.
The current paper proposes a method based on traditional least
squares parameter estimation. In a first step temporarily ordered point
clouds containing coordinates from each individual trajectory are
identified. For each point cloud, network adjustments and analyses are
carried out where outliers are identified using multiple t-testing.
Final coordinates are estimated using the remaining healthy observed
coordinates. Precision numbers are computed in the form of covariance
matrices or standard deviations. The method could find use in extracting
e.g. popular hiking trials from crowd sourced data, collecting
trajectories describing animal movement or in precise mapping av road
lines.
Section 2 gives a very short review of GNSS positioning in kinematic
mode highlighting different coordinate systems and reference frames as
well as stochastic information accompanying the coordinates. Section 3
is on the formation of discrete point clouds while section 4 gives the
theoretical outline of the proposed method. Section 5 presents
processing results using trajectories from a simulated dataset and
section 6 presents results from a more complex scenario where individual
trajectories have been measured using a GNSS multi-sport device.
Discussion and some suggestions for future work are presented in section
7 while section 8 contains conclusions.
2. GNSS KINEMATIC POSITIONING
In the GNSS device or GNSS software, raw observations in the form
of distance measurements between the GNSS receiver antenna and antennas
of GNSS satellites are used to estimate three-dimensional receiver
coordinates (x,y,z) along with nuisance parameters such as e.g. receiver
clock biases (e.g. Teunissen & Montenbruck, 2017). Estimated receiver
coordinates are Earth Centered Earth Fixed (ECEF) coordinates given in
the reference frame defined by the coordinates of satellites and
eventual differential reference stations. Using a handheld GPS-receiver,
satellite coordinates are normally obtained from the broadcasted
navigation message and coordinates are then referred to WGS84.
Broadcasted navigation messages from other GNSS-systems such as GLONASS,
Galileo and Beidou are using reference frames which are nearly identical
to ITRF (International Terrestrial Reference Frame), which again is
nearly identical to WGS84 (e.g. Teunissen & Montenbruck, 2017).
For most geomatic applications, three-dimensional Cartesian
xyz-coordinates in the ECEF coordinate system are converted to
planimetric coordinates (North, East) and height (e.g. Hofmann-Wellenhof
et al., 2008). The conversion from xyz-coordinates to North-, East-,
height-coordinates is a two-step procedure. The first step involves
conversion to latitude, longitude and ellipsoidal height related to a
reference ellipsoid. The last step involves conversion from latitude and
longitude to Northing and Easting in the mapping plane by applying an
appropriate mapping projection. Ellipsoidal heights are converted to
gravity based heights using corrections in the form of e.g. geoid
heights obtained from a geoid-model. If working with coordinates in a
regional reference frame, e.g. the European ETRF89, receiver coordinates
in the global WGS84 or ITRF should be transformed to the regional
reference frame. The transformation involves the time difference from
the epoch of observation to the reference epoch of the regional
reference frame as well as spatial differences between the reference
frames at the corresponding reference epochs (e.g. Nørbech & Plag,
2002). Most national mapping agencies supply transformation formulas and
software to transform and to convert GNSS-coordinates obtained from
single point GNSS positioning to the national reference frame.
Along with estimated receiver coordinates, accompanying
covariance-matrices are initially available from the GNSS processing.
The initial 3x3 covariance matrices for Cartesian ECEF-coordinate can be
converted to 3x3 covariance matrices for North-, East- and height
coordinates using the general law for error propagation (e.g. Ghilani,
2017). It should be pointed out that some GNSS devices and software
output full three-dimensional covariance information, some output
standard deviations only (ignoring correlations between estimated
coordinates) and some do not output any quality measures at all. When
working with trajectories, the height coordinates are normally ignored
as only horizontal coordinates are of interest. Covariance matrices
accompanying North- and East coordinates are then reduced to
2x2-matrices.
3. IDENTIFICATION OF DISCRETE POINTS CLOUDS ALONG THE TRAJECTORY
The proposed method is based on the fact that all points along a
trajectory have corresponding neighbor points in accompanying
trajectories. Our criteria for selecting corresponding neighbors for a
point in one trajectory is based on the minimum Euclidean distance to
points in the other individual trajectories. Typical sampling interval
of a GNSS-device is 1 second. The spatial distance between adjacent
points along a trajectory then depends on speed, typically 1.4 m/s for a
pedestrian (Levin & Norenzayan, 1999) and 13.9 m/s for a car travelling
at a speed of 50 km/h. To minimize the effect of sampling rate on the
choice of nearest neighbor, the spatial density of points along each
trajectory can be increased by e.g. linear interpolation. For
trajectories sampled by a handheld GNSS device with a horizontal
accuracy of 5 m (one sigma), a spatial distance of e.g. 0.05 m between
points along the trajectory will minimize the effect of sampling rate on
choice of neighbor points.
Following a densification of each individual trajectory, one
trajectory is selected as reference trajectory and for each point, a
search is carried out to find nearest neighbors in accompanying
trajectories.
Denoting the number of individual trajectories m and the spatial
distance between points along each trajectory d_dist, the clustering
algorithm will output a series of point clouds along the trajectory.
Each point cloud consists of m points and the distances between point
clouds are approximately d_dist.
The clustering process might be sensitive to the choice of initial
reference trajectory. The search for nearest neighbors can therefore be
iterated where e.g. weighted mean coordinates of each point cloud are
used as reference in a re-search for the m closest neighbors. Subsequent
re-clustered point clouds are then used to estimate and validate
outliers and to estimate coordinates along the final trajectory.
4. ESTIMATION AND VALIDATION
4.1 Estimation of coordinates and standard deviations
The suggested approach is based on least squares parameter estimation
(e.g. Ghilani, 2017). Independent estimation and analysis processes are
carried out for each point cloud along the trajectory. The number of
point clouds is denoted n and the number of points in each point cloud
is m. Cloud number is also an epoch number and is indicated with
subscript i, i=1,2,…., n. We use superscript j to indicate individual
points in each point cloud, j=1,2,…., m. Unknown parameters for each
point cloud are horizontal coordinates Ni and Ei. The coordinates of
each point in the point cloud, Nij and Eij are treated as observations
and the number of observations in one point cloud is thus 2m. The
observations are assigned weights using 2x2 covariance matrices, Σij,
accompanying each tuple of observed North- and East coordinates. In the
functional model, we express the observations as a function of the
unknown parameters.

, where vector l contains the observations in each point cloud, v
is vector with residuals, A is design matrix and x is vector with
unknown parameters.
Applied to our case, we get
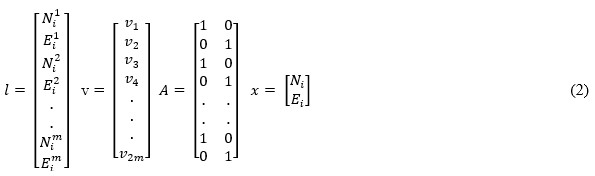
Due to lack of information, we ignore temporal correlations between
subsequent coordinate pairs in the stochastic model. If 2x2 covariance
matrices, Σij, for each pair of individual coordinates are available
from the GNSS processing, weight matrices for each pair of observations
are given by

The full weight matrix, W , is then a block diagonal matrix with
epoch wise 2x2 matrices wij along the diagonal.

The degrees of freedom, being the number of redundant observations,
is r = 2m – 2 for each point cloud.
Applying the principle of least squares gives us the estimated
parameters as

The vector with residuals is computed as

The standard deviation of unit weight is then

And standard deviations of estimated parameters can be computed as

Where q11 and q22 are respective diagonal elements in the cofactor
matrix Q

The covariance matrix of estimated coordinates is given by

As a measure of goodness of fit, the estimated standard deviation of
unit weight, s0, can be tested against the a priori value, σ0, using
the standard Chi-square test. Normally σ0=1 is used as a priori value.

If the computed χ2 is greater than the tabulated value with r
degrees of freedom and significance level of α (e.g. α=0.05), there is
a significant difference between a priori- and estimated standard
deviation of unit weight.
4.2 Extending the model to include outliers
Several methods have been developed in an effort to reduce the
influence of observational blunders. Traditional approaches for geodetic
measurements are based on attempts to detect, identify and remove
outliers (e.g. Baarda, 1968; Pope, 1976) or robust estimation designs to
mitigate the influence of outliers on the parameter estimates (e.g.
Huber, 1981). In this work, a relatively simple approach based on
multiple t-testing is presented (Pelzer, 1985; Asplan Viak, 1994). For
each single observation in the point cloud, we estimate an outlier as
one additional unknown parameter in the model described above. The
vector with observations, l , as well as the weight matrix, W , remain
as above while the design matrix A is extended with a new column to
accommodate the new outlier parameter.
The vector with unknowns is now

Where
 is the estimated outlier for observation number j in the
point cloud.
is the estimated outlier for observation number j in the
point cloud.
For the first observation (j=1), A is

Estimated parameters, residuals and standard deviations are computed
as given by eq.5 - eq.7. Standard deviation for the estimated outlier is
computed with

Where q33 is the third diagonal elements in the cofactor
matrix Q (eq. 10). For each observation, the number 1 in third column of
design matrix A is in a sequential manner interchangeably moved to each
observation to be tested, j=1,2,3,…,2m. A program run is carried out for
each observation (j), where estimated outliers
 with corresponding
standard deviations,
with corresponding
standard deviations,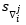 , are used to compute t-values
, are used to compute t-values

The t-values are T-distributed with r = 2m-3 ; degrees of freedom. As
the estimated outlier can have both positive and negative signs, this is
a two-sided t-test. Furthermore, when testing with a total significance
level of α (e.g. α = 0.05) the significance level of each individual
test has to be adjusted due to multiple testing. Assuming independent
observations, the significance level of each individual test, j, can be
computed by

If the number of observations to be tested is large (e.g. 2m >30 ), a
value of αj=0.001 is frequently used.
The outlier estimation and testing approach is a nested iterative
process. First the most extreme outlier is identified as being the
 associated with the largest computed
associated with the largest computed
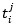 . This
. This
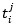 is
then checked against the tabulated T-value using r degrees of freedom
and significance level of
is
then checked against the tabulated T-value using r degrees of freedom
and significance level of
 . If the most extreme outlier is
significantly different to zero, the associated observed point is
removed and the whole procedure is repeated for the remaining
j=1,2,3,…,(2m-2) observations (e.g. Ghilani, 2017).
. If the most extreme outlier is
significantly different to zero, the associated observed point is
removed and the whole procedure is repeated for the remaining
j=1,2,3,…,(2m-2) observations (e.g. Ghilani, 2017).
The whole procedure is repeated until the most extreme outlier value
is not significantly different to zero. Final estimates and standard
deviations for coordinates are estimated using the remaining
observations.
Only the outlier parameter
 and associated standard deviation
and associated standard deviation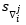 are required in the search for outliers. To speed up the
computations in an operational software, the somewhat naive approach of
estimating the full set of unknowns and standard deviations for every
observation to be tested can be replaced by an approach based on
Cholesky decomposition and back solution of an extended system of
equations (e.g. Asplan Viak, 1994 ; Leick et al., 2015).
are required in the search for outliers. To speed up the
computations in an operational software, the somewhat naive approach of
estimating the full set of unknowns and standard deviations for every
observation to be tested can be replaced by an approach based on
Cholesky decomposition and back solution of an extended system of
equations (e.g. Asplan Viak, 1994 ; Leick et al., 2015).
5. SIMULATED TRAJECTORIES
In this section the proposed method is used to estimate a trajectory
based on a simulated dataset. A “true” reference trajectory is made up
from line-segments connecting 11 control points, see figure 1. Distances
between adjacent control points are approximately 7 meters. Four
simulated trajectories are now computed.
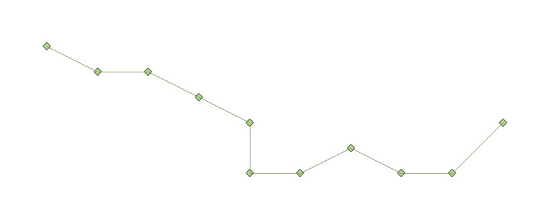
Figure 1. True
trajectory. Approximate distances between adjacent points are 7 meters.
Around each of the 11 control points, coordinates of four randomized
points are generated using the Matlab “randn-function” (Matlab Release
2018a, 2018). The Matlab “randn-function” returns normally distributed
random numbers. A standard deviation of 1 m is used in the generation of
each randomized coordinate, North and East respectively. Line-segments
connecting individual points in each cluster finalize the four simulated
trajectories, see figure 2.
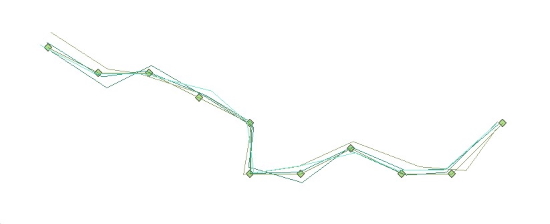
Figure 2. Four
simulated trajectories shown together with the true trajectory.
We now attempt to reconstruct the reference trajectory from the four
simulated trajectories. Along each simulated trajectory, densified
trajectories are generated using linear interpolation. Intermediate
distances along the four resampled trajectories are 0.05 m. As described
in section 3, the minimum Euclidian distance principle is now used to
identify a total of 2213 discrete point clouds along the resampled
trajectories. The estimation and validation scheme described in section
4 is used to estimate a best fit trajectory based on the four simulated
trajectories. Figure 3 shows the original reference trajectory along
with the estimated trajectory from a program run where the outlier
detection algorithm has not been applied. As seen from figure 3 along
with figure 2, the estimated trajectory fits the reference trajectory
better than each of the individual trajectories.
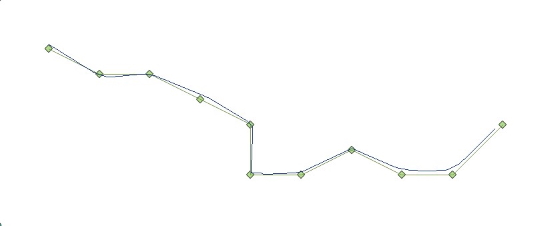
Figure 3. Trajectory estimated without application of outlier
detection, shown together with true trajectory.
Figure 4 shows the estimated trajectory stemming from a program run
were also the outlier detection algorithm was applied. 261 of the total
8852 “observed” coordinate-pairs (2.9 %) were detected as outliers and
omitted in the estimation of the final estimated coordinates that
constitute the trajectory. It can be observed that the occasional
detection of outliers along the estimated trajectory results in small
jumps.
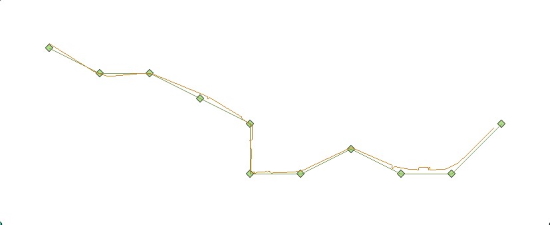
Figure 4. Trajectory estimated with application of outlier
detection, shown together with true trajectory. Occasional small jumps
can be seen along the estimated trajectory.
Table 1 presents some details concerning the estimated standard
deviations for estimated coordinates along the trajectory.

In this simulated dataset, estimated North- and East coordinates have
identical standard deviations. As the same random algorithm is used in
the simulation of both North- and East coordinates, the associated
estimated standard deviations have the same magnitude. As expected, the
minimum and mean of estimated standard deviations are smallest for the
program run with outlier detection.
5. TRAJECTORIES COLLECTED WITH A GARMIN FORERUNNER 910XT MULTI SPORT
DEVICE.
A Garmin Forerunner 910XT Multi Sport device is used to log positions
while running a loop of approximately 4.7 kilometer, see figure 5. The
device operated in the default data recording mode of smart recording
(Garmin, 2014). In smart recording mode, positions are recorded based on
a proprietary algorithm for change in direction, speed or hearth rate.
The data files are then smaller compared to the alternative setting of
recording positions every 1 second. Inspecting the resulting data files,
reveals that the recording interval vary between 1 second and ca. 10
seconds. With an average pace of approximately 6 minutes per kilometer,
there is a recorded position approximately every 2.8 – 28 meter. The
majority of the recordings are sampled approximately every 2-3 seconds /
5.6-8.4 meter respectively.
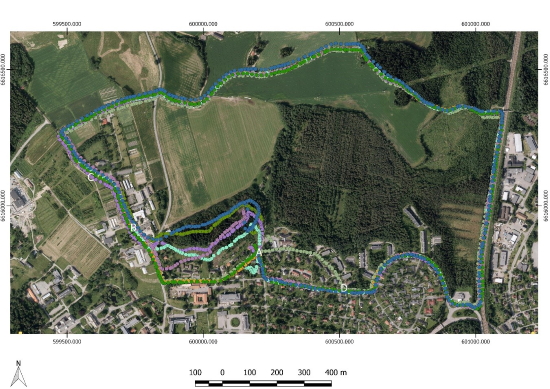
Figure 5. Plot of eight individual trajectories. Locations
mentioned in the description of artifacts a, b, c and d are shown with
white capital letters.
A total of eight runs started and ended at approximately the same
location A, see figure 5. The eight trajectories are run clockwise and
distributed in time over a period of more than one year, see table 2
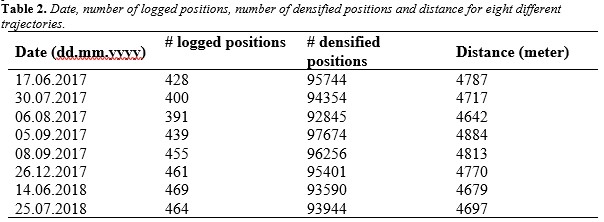
Some artifacts can be seen from figure 5 and are due to:
A. It is a well-known issue with the Garmin
Forerunner 910XT device that the first recorded positions occasionally
have errors of several tens of meters. The possibility of erroneous
first positions is higher if the device has not been used for a while.
B. From the starting point A to approximately point
B, the runner chose three different paths. Four of the runs started off
in a south-west direction, following the road. Two of the runs first
followed the road in a northern direction from the starting point A
before turning in a western direction following a foot-path through the
forest. Finally two of the runs selected a foot-path that goes between
the other two initial choices.
C. From approximately point B to approximately
point C, the runs chose slightly different paths. Some runs followed the
road while the others followed a footpath. The footpath runs
approximately 10-30 meters to the right of the road. This is in an area
with tall threes and thick foliage.
D. In the end of the loop from point D, returning
to the approximate start- and end-point A, seven of the runs followed
the same path. One run did however choose a complete different road to
the north of the other runs.
In the data processing, the artifacts concerning some of the
individual trajectories are not taken into concern, and the proposed
method is used to estimate coordinates for a best fit trajectory along
with quality data in the form of estimated standard deviations (eq. 5
and eq. 8-9). The recorded data are downloaded from the device and
converted to files with coordinates in the ETRF89 reference frame using
the UTM map projection in zone 32. The Garmin Forerunner 910XT device
does not provide any quality measures of logged positions. Assuming
equal accuracy for independent North- and East coordinates and an
horizontal accuracy of approximately 5 meters (e.g. van Diggelen &
Enge, 2015), a priori standard deviations σN,GNSS and σE,GNSS are both
assigned a value of 3.5 meter. To take into account that different runs
occasionally follow slightly different paths, e.g. left side of a road
on some runs and right side of the same road on other runs, the standard
deviation designated each observed coordinate is augmented with a term
that takes offsets between physical paths into account. Assuming that
errors are random and that GNSS errors are independent from track-offset
errors, a priori standard deviations for track-offsets, σN,Track and
σE,Track are used in the propagation of a priori final variances:
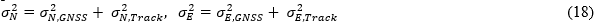
Where
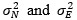 are a
priori variances for North- and East coordinates respectively and
subsequently used in the weighting scheme by populating the 2x2
covariance matrices,
are a
priori variances for North- and East coordinates respectively and
subsequently used in the weighting scheme by populating the 2x2
covariance matrices,
 , in
eq. 3. In the present estimation and analysis,
, in
eq. 3. In the present estimation and analysis,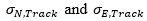 are both assigned
values of 2 meters.
are both assigned
values of 2 meters.
Each trajectory is first resampled to a distance of 0.05 m between
adjacent points. The minimum Euclidian distance principle as described
in section 3 is then used to identify a total of 94 354 discrete point
clouds along the trajectory before the estimation and validation scheme
suggested in section 4 is used to estimate the final trajectory. A
program run without the outlier detection algorithm averages out the
effects of the artifacts mentioned above and estimated coordinates and
trajectory from this approach is not shown here. In figure 6, the
background orthophoto is removed and shows the estimated coordinates
from a program run were the outlier detection algorithm is applied. A
first glance at figure 6 reveals two interesting observations:
- In the beginning of the loop, from the starting point A to
approximately point B, there is only small segments of estimated
coordinates as the outlier detection has rejected most of the
observed coordinates. Estimated coordinates for the small segments
in this first part have associated standard deviations of several
tens of meters.
- In the end of the loop, from point D to the start- and end-point
A, the estimated trajectory follows the main path defined by seven
of the runs. The deviated path of the one single run is rejected by
the outlier detection approach.
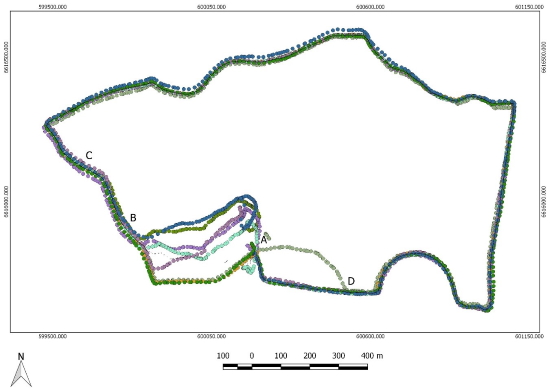
Figure 6. Plot of estimated trajectory from a program run with
outlier detection algorithm applied. The estimated trajectory is shown
as a thin black line together with the eighth individually observed
trajectories. Compared with figure 5 the background orthophoto is
removed in order to better see poorly estimated segments. Locations
mentioned in the description of artifacts a, b, c and d are shown with
capital letters.
The combined effect of artifacts a, b and c, mentioned above, is that
one common trajectory is not justified for the start segment from point
A to point B and further on to point C. As seen in figure 6, the
proposed estimation and validation scheme has nevertheless produced
short segments of a trajectory in this first part. The reason why not
all observations have been rejected in this part, is that the outlier
detection approach has not been able to distinguish between “good
observations” and “bad observations”. All observations have passed the
t-test, but estimated coordinates are associated with very high standard
deviations. In the final step, a filter based on the outcome from the
test of estimated standard deviation of unit weight (eq. 12) is
therefore used to reject poorly estimated coordinates.
Figure 7 shows the final accepted trajectory with a thin line.
Segments filtered out by the Chi-square test are marked with thicker
black dots.
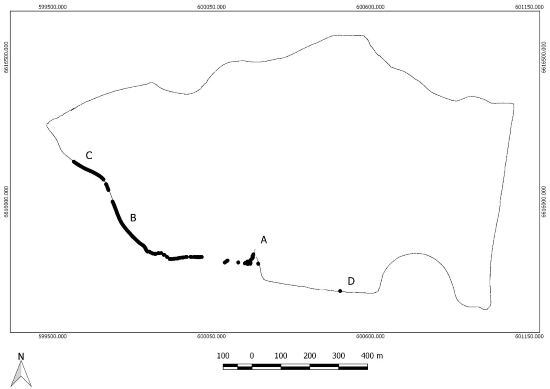
Figure 7. Plot of estimated trajectory from a program run with
outlier detection algorithm applied. Accepted trajectory with a thin
line and segments rejected in the Chi-square test with thicker black
dots. Locations mentioned in the description of artifacts a, b, c and d
are shown with capital letters.
Concerning artifact d, the outlier detection algorithm effectively
detected that the path selected by one run significantly diverges from
the path selected by all the other runs. Table 3 gives maximum, minimum
and mean standard deviations for estimated coordinates for accepted and
rejected coordinates respectively. In the stochastic model, we have for
the current dataset assumed that observed North- and East coordinates
are independent of one another. Since there is no common information
between estimated North- and East coordinates in the functional model,
all standard deviations are then equal for estimated North- and East
coordinates.

Figure 8 shows cumulative distribution plots of standard deviations
for accepted and for rejected coordinates. For the accepted coordinates,
the largest standard deviation is approximately 2.1 m, and 95% of
standard deviation are smaller than 1.5 m. For the rejected coordinates,
the largest standard deviation is approximately 21.3 m, and 5% of
standard deviations are larger than 20.2 m.
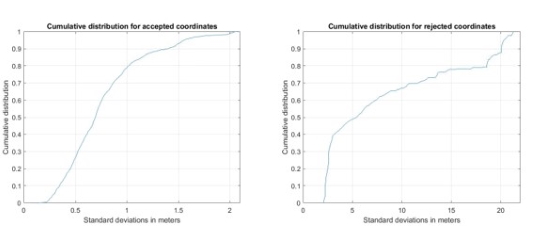
Figure 8. Cumulative distribution for North- or East-coordinates
for accepted points left and rejected points right.
7. DISCUSSION AND SOME SUGGESTIONS FOR FUTURE WORK
Detection and removal of occasional outliers introduce sudden small
jumps in the estimated trajectory, as seen in figure 4 in the section
with the simulated dataset. Depending on the actual application, there
can be a need to smooth out such inconsistences. The handling of
practical aspects does also deserve attention, e.g.:
- methods and techniques on how to fill in gaps in estimated
trajectories,
- interpolation techniques when densifying the original
trajectories, e.g. linear interpolation or splines,
- optimization of computational speed,
- datasets with individual trajectories where some observers
choose to go left of an obstacle, e.g. a lake, and other choose go
right,
- datasets with very curved trajectories,
- datasets with nested trajectories.
Finally, alternative methods for dealing with outliers as well as the
acceptance criteria for automatically rejecting segments with “bad”
observations are interesting topics. E.g. when estimating the trajectory
of centerlines of roads, a stricter acceptance criteria is required
regarding choice of the same physical path than for e.g. hiking trials.
This proximity requirement can for different applications be managed by
tuning the augmentation of the a priori covariance matrices
 for
observed coordinate (eq. 18). Assigning smaller track-offset terms (e.g.
center lines of roads) will make the goodness of fit test (eq. 12) more
sensitive to diverging paths than larger track-offset terms (e.g. hiking
trials). How to assign proper track- offset values,
for
observed coordinate (eq. 18). Assigning smaller track-offset terms (e.g.
center lines of roads) will make the goodness of fit test (eq. 12) more
sensitive to diverging paths than larger track-offset terms (e.g. hiking
trials). How to assign proper track- offset values,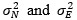 , to take into account required proximity for individual
physical paths should be further explored.
, to take into account required proximity for individual
physical paths should be further explored.
8. CONCLUSIONS
In this work, a method is proposed on how to automatically estimate
one best fit trajectory from several individually measured trajectories.
The proposed method uses a weighted least squares approach to take into
account a priori accuracies and correlations of individual trajectories.
An outlier detection algorithm based on multiple t-testing is used to
isolate and omit bad observations. The outlier detection algorithm might
also detect if any selected paths significantly deviates from other
choices of paths. Remaining segments of bad observations or multiple
choices of paths can be identified by applying a final filter based on a
statistical test of goodness of fit.
The final product is a trajectory consisting of a temporally sequence
of coordinates. Each estimated coordinate has an associated quality
number in the form of a standard deviation. Due to erroneously observed
coordinates or choice of multiple diverging paths during data
collection, there might be gaps in the final trajectory. Eventual gaps
can subsequently be flagged and give information on that additional
measures must be used to finalize the trajectory. The proposed method
can be applied to trajectories from different sources. E.g. trajectories
in existing databases can be combined with newly observed trajectories.
The difficult task then is how to assign proper a priori stochastic
information to the different trajectories, ideally in the form of full
variance-covariance information.
REFERENCES
- Asplan Viak IT. (1994). Gemini Net/GPS-Brukerhåndbok. Asplan
Viak Informasjonsteknologi A.S. (in Norwegian)
- Baarda, W. (1968). A testing procedure for use in geodetic
networks. Netherlands Geodetic Commission, Publications on Geodesy,
New series Vol.2 No 5. Delft.
- Buchin, K., Buchin, M., van Kreveld, M., Löffler, M., Silveira,
R.I., Wenk, C., & Wiratma, L. (2013). Median Trajectories.
Algorithmica, 66, 595-614.
- Garmin, (2014). Garmin Forerunner 910XT Owners Manual. Garmin
Ltd 2014, available from
http://static.garmin.com/pumac/Forerunner_910XT_OM_EN.pdf, (accessed
on 21.01.2019).
- Ghilani, C.D. (2017). Adjustment Computations: Spatial Data
Analysis. 6th. Edition, Wiley. Hofmann-Wellenhof, B., Lichtenegger,
H., Wasle, E. (2008). GNSS – Global Navigation Satellite Systems.
Springer.
- Huber, P.J. (1981). Robust statistics. Wiley, New York. Leick,
A., Rapoport, L., Tatarnikov, D. (2015). GPS Satellite Surveying,
fourth edition. John Wiley Sons.
- Levine, R.B., Norenzayan, A. (1999). The Pace of Life in 31
Countries. Journal of Cross-Cultural Psychology, Vol. 30, No. 2,
178-205.
- Matlab Release 2018a. The MathWorks, Inc. (2018), Massachusetts
United States, available from
https://se.mathworks.com/help/matlab/index.html (accessed on
19.02.2019).
- Nørbech, T., Plag, H.P. (2002). Transformation from ITRF to
ETRF89(EUREF89) in Norway. EUREF Publication No. 12, Mitteilungen
des Bundesamtes für Kartographie und Geodäsie, pp. 217-222. Verlag
des Bundesamtes für Kartographie und Geodäsie, Frankfurt am Main.
- Pelzer, H. (1985). Geodätische Netze in Landes- und
Ingenieurvermessung. Vorträge des Kontakstudiums II. Wittwer Verlag.
(in German)
- Pope, A. (1976). The statistics of residuals and detection of
outliers. NOAA Technical Report, NOS 65 NGS 1. Rockville.
- Teunissen, P.J.G., Montenbruck, O. (2017). Springer Handbook
of Global Navigation Satellite Systems. Springer.
- van Diggelen, F., Enge, P. (2015). The World’s first GPS MOOC
and Worldwide Laboratory using Smartphones, Proceedings of the 28th
International Technical Meeting of The Satellite Division of the
Institute of Navigation (ION GNSS+ 2015), Tampa, Florida, September
2015, pp. 361-369.
- Vaughan, N., Gabrys, B. (2016). Comparing and combining time
series trajectories using Dynamic Time Warping. 20th International
Conference on Knowledge Based and Intelligent Information and
Engineering Systems, KES206, 5-7 September 2016, York, United
Kingdom, Procedia Computer Science 96, 465-474.
BIOGRAPHICAL NOTES
Ola Øvstedal is an Associate Professor at the
Section of Geomatics, Faculty of Science and Technology, Norwegian
University of Life Sciences. He received his PhD in geodesy in 1991.
Current research interest are satellite positioning and estimation
techniques. He is a national delegate to FIG Commission 5 “Positioning
and Measurements”.
CONTACTS
Ola Øvstedal Section of Geomatics, Faculty of Science and Technology
Norwegian University of Life Sciences
P.O.Box 5003, N-1432 Ås, Norway
Tel: +47 67231549
Web site: https://www.nmbu.no/en