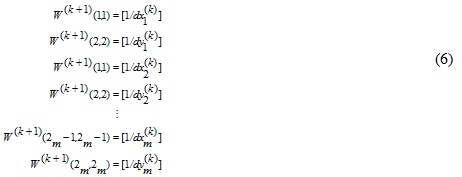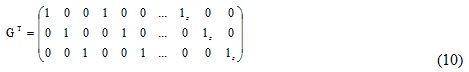Article of the Month -
April 2014
|
A Practical Deformation Monitoring Procedure and Software System for
CORS Coordinate Monitoring
Meng Chan LIM and Halim SETAN, Malaysia
1) This paper illustrates the
combination of continuous GPS measurement with robust method for
deformation detection to GPS station position change. A window-based
software system for GPS deformation detection and analysis via robust
method, called Continuous Deformation Analysis System (ConDAS), has been
developed at Universiti Teknologi Malaysia. This paper describes the
design and architecture of ConDAS and highlights the deformation
analysis results from two assessments. The paper is a Malaysian Peer
Review paper, which will be presented at FIG Congress 2014 16-21 June,
in Kuala Lumpur, Malaysia.
SUMMARY
This paper illustrates the combination of continuous GPS measurement
with robust method for deformation detection to GPS station position
change. A software system named Continuous Deformation Analysis System
(ConDAS) has been developed at Universiti Teknologi Malaysia. It was
specially designed to work with high precision GPS processing software
(i.e. Bernese 5.0) for coordinate monitoring. The main components of
ConDAS are: parameter extraction (from Bernese output), deformation
detection (via IWST and S-transformation) and graphical visualisation.
Two assessments were included in this paper. Test results show that the
system performed satisfactorily, significant displacement can be
detected and the stability information of all monitored stations can be
obtained. This paper highlights the architecture, the design of the
software system and the results.
1. INTRODUCTION
Continuous Global Positioning System (GPS) networks record station
position changes with millimetre-level accuracy have revealed that GPS
is capable of detecting the significant deformations on various spatial
and temporal scales (Ji and Herring 2011; Li and Kuhlmann 2010; Cai et
al. 2008; Yu et al. 2006). However, a rigorous deformation analysis
technique is still required for preparing a versatile and comprehensive
spatial displacement results. To date, several continuous deformation
monitoring systems are operational, such as SCIGN (Hudnut et al. 2001),
GOCA (Jager et al. 2006) and DDS (Danisch et al. 2008). This study
employs a robust method known as Iteratively Weighted Similarity
Transformation (IWST) and final S-Transformation to the daily GPS
position time series.
A window-based software system for GPS deformation detection and
analysis via robust method, called Continuous Deformation Analysis
System (ConDAS), has been developed at Universiti Teknologi Malaysia. It
is a software system that solely designed to work with high precision
GPS processing software (i.e. Bernese 5.0) for coordinate monitoring.
The main components of ConDAS are: parameter extraction (from Bernese
output), deformation detection and graphical visualisation. All these
components are integrated in one environment using MATLAB.
This paper describes the design and architecture of ConDAS and
highlights the deformation analysis results from two assessments. In
fact, the robust IWST method that employed by ConDAS is typically used
for structural deformation monitoring such as dam, slope and etc.
However, this study combines IWST and final S-Transformation techniques
to Continuous Operating Reference Station (CORS) coordinate monitoring.
Larger monitoring area was analysed using robust method for the first
time. Promising results have been obtained through the assessment.
2. SYSTEM DEVELOPMENT APPROACH
This study is devoted to develop a software system that adapts to GPS
deformation detection and analysis for GPS CORS network. Due to the
extraordinary demands for displacement detection accuracy, high
precision GPS processing software, namely Bernese 5.0 is employed.
Figure 1 outlines the process of entire study.

Figure 1: The outline of developed deformation detection system
ConDAS is designed to work with Bernese software for deformation
detection and analysis, thus this study comprises of two parts: GPS data
processing strategy (via Bernese) and deformation analysis strategy (via
ConDAS).
2.1 GPS Data Processing Strategy
There are numbers of GPS deformation monitoring study using Bernese
to process GPS data (Haasdyk et al. 2010; Hu et al. 2005; Jia 2005;
Janssen 2002; Vermeer 2002). By implementing the Bernese software, data
cleaning, cycle slip detection, ambiguity resolution and network
adjustment of GPS data all can be achieved to meet the desired criteria.
The processing procedure using Bernese Processing Engine (BPE) with
double difference is illustrated in Figure 2.
Basically, the entire GPS processing step is divided into three
parts: preparation, pre-processing and processing. The preparation part
deals with computing a priori coordinate file, preparing the orbit and
earth orientation files in Bernese formats, converting RINEX files to
Bernese format, synchronising the receiver clocks to GPS time and
producing an easy to read overview of available data. Meanwhile, the
pre-processing part handles the creation of single difference files,
editing of the cycle slips and removal of suspect observation. The
processing part is responsible to resolve the ambiguity. After computing
a solution with real valued ambiguities the Quasi Ionosphere Free (QIF)
strategy is used to resolve ambiguities to their integer numbers.
Subsequently, the processing part computes and provides the fixed
ambiguity solution. A summary results file is saved and dispensable
output files are removed at the final stage of processing.

Figure 2: Double difference GPS processing method using BPE
The GPS data are post-processed using Bernese 5.0 software. In order to
capitalise the deformation analysis context, some GPS data processing
parameters and models were carefully configured as listed in Table 1. In
spite of the general script in Bernese GPS software 5.0, some processing
scripts are slightly change to well fit the requirement of deformation
analysis. For instance, the function of script SNGDIF (in the
pre-processing part) is used to generate single-difference files from
two zero-difference files. In other word, program SNGDIF is employed to
form baselines only from zero-difference observation files. There are
plenty of options to be selected for generating the single-difference
observation files for network solution. In general the option OBS-MAX
guarantees the best performance for the processing of a network using
correct correlations. However, there is another option that fit the
demand of deformation analysis, called DEFINED option, in which only the
predefined baselines from a baseline definition file are created. The
selection of DEFINED option has significant impact on the determination
of total number of parameters involved for every epoch.
Table 1: Parameters and models used in GPS data processing

Generally, Bernese GPS Software allows user to control the processing
strategies or even skip certain redundant scripts (highlighted in Figure
2) during processing. Thus, for deformation analysis purpose, the
following redundant scripts are skipped: HELMR1, R2S_SUM, R2S_SAV and
R2S_DEL.
Besides, the command line of searching clock correction file
(P1C1yymm.DCB and P1P2yymm.DCB) had been removed or disable from the
R2S_COP script that stored in the directory C:\GPSUSER\SCRIPT.
Eventually, the GPS data processing was performed without the clock
correction file and it has been verified that no significant influence
on final Bernese output by incessant trial and error. At last, three
types of result files were generated for every 24-hour epoch, for
instance: a priori coordinate file and adjusted coordinate file in STA
folder (e.g.: APR110010.CRD & R1_110010.CRD), along with covariance file
in OUT folder (e.g.: R1_11001.COV).
2.2 Deformation Analysis Technique and Software Development
The determination of deformations is mainly formed from two parts.
The first is the measurement of deformation and the second is the
analysis of these measurements (Aguilera et al. 2007). However,
deformation analysis using the geodetic method mainly consists of a
two-step analysis via independent adjustment of the network of each
epoch, followed by deformation detection between the two epochs (Setan
and Singh 2001). In this case, network adjustment is handled by Bernese
5.0 software and ConDAS carries out the two-epoch deformation analysis.
Generally, conventional deformation analysis applied in geodesy
(Caspary 1988) extracts the deformation vectors and the
variance-covariance matrix. In this classification, Iteratively Weighted
Similarity Transformation (IWST) tends to compute the displacement
vector and its variance-covariance matrix by iteratively changing weight
matrix, W. In fact, IWST method belongs to the family of “robust”
methods. IWST method finds the best datum, with minimal distorting
influence on the vector of displacement (Chrzanowski et al. 1994).
However, for the deformation analysis here we strongly recommended the
final S-transformation (with respect to stable reference points) after
the IWST is applied. A flow chart of IWST with final S-Transformation
method is illustrated in Figure 3. For further computation of IWST and
S-Transformation, please refer to Lim (2012), Lim et al. (2010) and Chen
et al. (1990).
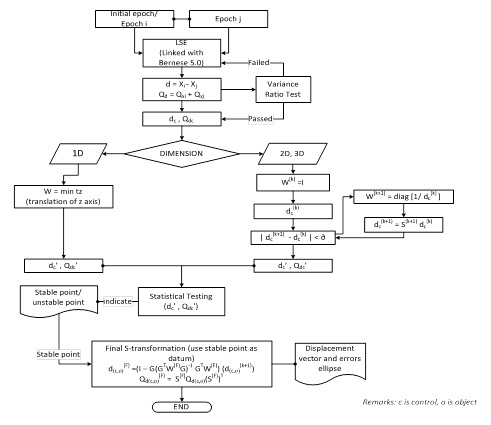
Figure 3: Flow chart of IWST with final S-Transformation that deployed
in ConDAS
Two-epoch deformation analysis was employed in this study. From
Figure 3, when comparing the two epochs of data (Epoch i: Xi , Qx ;
Epoch j: Xj , Qx ) , the vector of displacements (dc) and (Qdc) its
cofactor matrix are calculated as shown in Lim et al (2010):

(In Equations (1) and (2), Xi and Xj must be in the same datum. An
S-transformation with respect to the same datum must be conducted before
the calculation of d (Figure 3).
At the beginning of the deformation analysis, the first matrix which
must be computed is the weight matrix, W. For the first iteration (k=1),
the matrix W is equal to I (i.e. W=I), where all the diagonal elements
are 1 and all other elements are 0. In the second (k+1) and all
subsequent iterations, the diagonal elements of the weight matrix are
defined as:

For 1-D networks, there are some differences for the calculation of
d’ and Qd’. Firstly, the displacements d are arranged in increasing
order. The median is assigned unit weight 1 and zero weight is assigned
to the other displacements d. If the total number of d is an even
number, the two middle (median) displacements d are assigned unit weight
1 and zero weight is assigned to the other displacement d (Chen et al.
1990). Then, the new vector of displacements d’ and its cofactor matrix
Qd’ are (Chen et al. 1990):

where tz = mean value of the middle displacements and
di = the displacement of point i.
S = similarity transformation matrix =
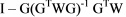
G = inner constraint matrix
For a 2-D network, the elements of the weight matrix W are computed
as follow:
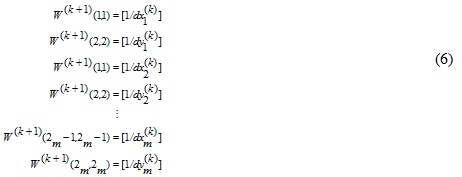
where k is the iteration number.
For a 3-D network, the elements of the weight matrix W are computed
as follow:

It is possible that some
 may approach zero
during the iterations, causing numerical instabilities, because may approach zero
during the iterations, causing numerical instabilities, because
 becomes very
large. There are two ways to solve this problem (Chen et al. 1990): becomes very
large. There are two ways to solve this problem (Chen et al. 1990):
i. Setting a lower bound (e.g. 0.0001 m). If
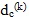 is smaller than
the lower bound value, its weight is set to zero, or is smaller than
the lower bound value, its weight is set to zero, or
ii. Replacing the weight matrix as
 , where , where
 is a tolerance
value. is a tolerance
value.
In this study, the first solution has been chosen and it is preferable
to limit the weight matrix for avoiding the long computation.
After that, 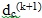 is
computed using the following equation (Chen et al. 1990) is
computed using the following equation (Chen et al. 1990)

The G matrix is an inner constraint matrix. The dimensions of the G
matrix are different for 1-D, 2-D and 3-D networks. For a GPS network,
the matrix G is illustrated as Equation 10.
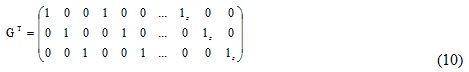
Further details are given in Chen et al. (1990) and Chrzanowski et
al. (1994). The iterative procedure continues until the absolute
differences between the successive transformed displacements d are
smaller than a tolerance value
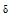 , 0.0001 m (Chen
et al. 1990): , 0.0001 m (Chen
et al. 1990):

In the last iteration, a final S-transformation is performed to get
the actual value of the displacement vector by using stable reference
points (as verified by the previous IWST analysis) as datum.
Consequently, elements of weight matrix, W are assigned 1 for stable
reference points and 0 for other points to achieve the final
S-transformation. Hence, the principle of congruency testing (Setan and
Singh, 2001) is used for calculating the actual deformation displacement
vector. In the final iteration, the displacement vector
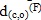 and the final
cofactor matrix and the final
cofactor matrix 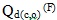 of
displacement vector are computed as: of
displacement vector are computed as:

where 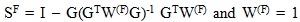 for
stable reference points and 0 for other points based on the previous
IWST analysis. for
stable reference points and 0 for other points based on the previous
IWST analysis.
When the vectors of the displacements and the variance-covariance
matrix of each point are computed, the stability information of each
point can be determined through a single point test. The displacement
values and the variance-covariance matrix are compared with a critical
value. Assuming the point i is tested, then, the algorithms are as
follow (Chen et al. 1990; Setan and Singh 2001)
:
where

If the above test passes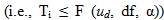 then the point is assumed to be stable at a significance level α.
Otherwise, if the test fails
then the point is assumed to be stable at a significance level α.
Otherwise, if the test fails
 then the point is
assumed to have moved. then the point is
assumed to have moved.
In principle, ConDAS has been developed using Matrix Laboratory
(MATLAB). This software system is tentatively developed to detect the
unstable stations in a deformation monitoring network by IWST method and
S-Transformation to analyse the GPS results in the deformation
perspective. Figure 4 illustrates the overall workflow of ConDAS.

Figure 4: Architecture of ConDAS (Lim et al., 2011)
As an overall, ConDAS consists of three modules: parameters
extraction module, deformation detection module and visualisation
module. The architecture and function of modules are described
respectively as following.
2.2.1 Parameters Extraction Module
After high accuracy coordinates computation from Bernese GPS
software, a posteriori variance factor, degree of freedom and
variance-covariance matrices can be obtained from the result files.
These parameters are required in order to perform the two-epoch
deformation analysis. In other words, these parameters are the inputs of
deformation analysis. For this study, a Bernese parameter extraction
module has been created using MATLAB as illustrated in Figure 5(a). It
was designed to suit with Bernese in order to extract the required
parameters according to the format of Bernese results files. A warning
message will pop out if the specify parameters are unavailable in the
Bernese output file. A deformation input file in text file (.txt) was
generated after parameters extraction from Bernese output as shown in
Figure 5(b).
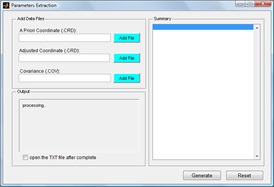
Figure 5(a): GUI of parameters extraction |
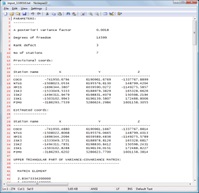
Figure 5(b): Example format of deformation input file. |
2.2.2 Deformation Detection Module
The core of deformation analysis program is the implementation of
IWST algorithm. However, initial checking of data and test on variance
ratio are important to ensure that common points, similar approximate
coordinates and same points names are used in two epochs. Thus, there is
a statistic test termed variance ratio test that need to be conducted in
order to determine the compatible weighting between two epochs, and any
further analysis should be stopped at this stage if test is rejected.
The test statistic is referred to as Equation 15 (Lim et al. 2010; Setan
and Singh 2001).

with j and i represent the larger and smaller variance
factors, F is the Fisher’s distribution, is the chosen
significance level (typically = 0.05) and
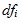 and and
 are the degrees of
freedom for epoch i and j respectively. are the degrees of
freedom for epoch i and j respectively.
In this module, two-epoch deformation analysis were performed in two
stages: i) stability analysis of reference stations using IWST and
single point test; and ii) deformation analysis of all stations by final
S-transformation and single point test. Indication of a set of stable
control stations was crucial in order to compute the displacement
vectors of all monitored stations respectively. Deformation detection
module of ConDAS as illustrated in Figure 6(a) currently utilises a
single point test in detecting displacement that reject any point with
its displacement extends beyond the confidence region (Chrzanowski et
al. 1994). It is flagged as unstable if a given point fails the test at
the specified confidence level. At the final stage of program, a
summarised deformation output file could be generated as shown in Figure
6(b). It contains the summary of file used, statistical summary and
station information whether the station is flagged as moved or stable.
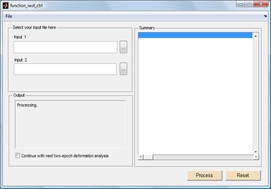
Figure 6(a): GUI of deformation detection module |
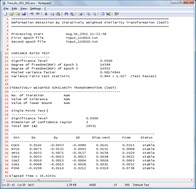
Figure 6(b): Output file of deformation detection module |
2.2.3 Visualisation Module
The function of the visualisation module is twofold: i) to view the
stability results of every two-epoch analysis; ii) to generate the
deformation trend over a selected period. In fact, the stability results
in numerical and graphical modes are provided and visualised together
with error ellipse and displacement vector for every monitored station.
Besides, fluctuation of displacement vector over a period can be
visualised via this module. Some data statistics (e.g.: maximum, minimum
and standard deviation values over that particular period) also can be
obtained from visualisation module. Figure 7 presents the GUI of
visualisation module
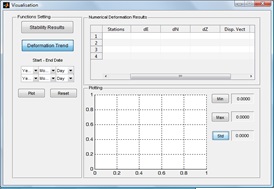
Figure 7: GUI of visualisation module.
3. TEST RESULTS
Two test results were included in this paper for assessment purpose.
Due to the CORS coordinate monitoring is the aim of the study, two sets
of GPS data were collected from Malaysia Real Time Kinematic GNSS
Network (MyRTKnet) and Iskandar Malaysia CORS Network (ISKANDARnet)
(Shariff et al. 2009). The first set of data was used to validate the
software system by Aceh earthquake incident, the latter one was utilised
to monitor the displacement trend of every GPS stations within the
network.
3.1 Test Results 1: Validation of System using Aceh Earthquake
Lately, the validation of the entire system was conducted by using
the existing GPS data set from MyRTKnet. The processed data set started
from 4th Dec 2004 until 31st Dec 2004 (i.e. before and after the Aceh
earthquake incident on 26th Dec 2004). Total six of IGS stations (ALIC,
DARW, DGAR, HYDE, KARR and KUNM) have been chosen as the control points
and two stations from MyRTKnet: JHJY and LGKW were selected as object
points. Figure 8 illustrates network distribution of selected IGS and
MyRTKnet stations.
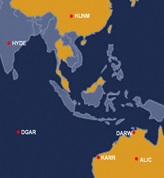

Figure 8: Network distribution of six IGS stations and two MyRTKnet
stations
However, only the stable control point (among the selected IGS
station) that being verified by ConDAS can be used as datum to compute
the displacement vectors of object points. Throughout the analysis, all
stations were stable before the earthquake happen. However, the results
show the LGKW station was moved start from 26th Dec 2004 and onwards.
These results are similar with findings from Jhonny (2010). Figures 9
and 10 illustrate the fluctuation of displacement vectors for JHJY and
LGKW.
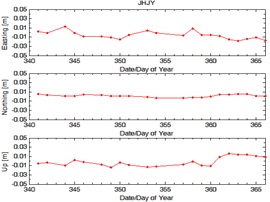
Figure 9: Fluctuation of displacement vectors of station JHJY in
Easting, Northing and Up. |
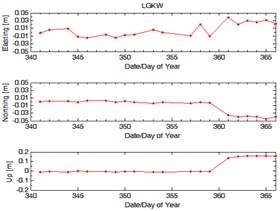
Figure 10: Fluctuation of displacement vectors of station LGKW
in Easting, Northing and Up. |
From Figure 9, there were no significant movements detected at
station JHJY during the incident occurred and the days onwards. The
maximum displacement vectors were varied from 0.003m to 0.023m. However,
significant movements were detected at station LGKW at the day of year
361 and onwards (Figure 10). The displacement vectors were diverged from
0.007m to 0.167m. Table 2 shows the stability information in numerical
results.
Table 2: The displacement vectors of
station JHJY and LGKW
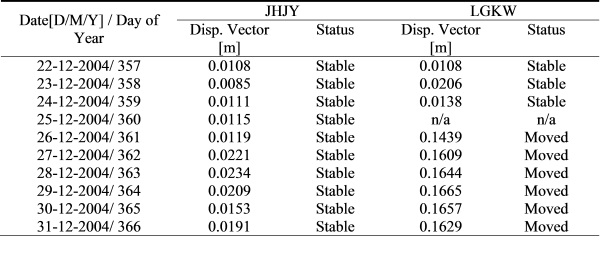
n/a = data not available
3.2 Test Results 2: Deformation Trend of ISKANDARnet
There were seven stations in the deformation monitoring network, four
from the IGS stations were used as reference (i.e. COCO, NTUS, PIMO,
XMIS) and three stations from ISKANDARnet (ISK1, ISK2 and ISK3) were
used as object points as illustrated in Figure 11.

Figure 11: The deformation monitoring network for ISKANDARnet
GPS data processing and two-epoch deformation analysis were performed
using two years (1st Jan 2010 – 31st Dec 2011) GPS data. However,
ISKANDARnet was undergone some rigorous on-site maintenance during
March, July and August of year 2010 and early of April until Jun of year
2011. Thus, no GPS data was available on that specified period. After
the GPS data processing was carried out with Bernese software, two-epoch
deformation analysis (at 5% significance level) were performed in two
stages: i) stability analysis of reference stations using IWST; and ii)
deformation analysis of all stations. The stability of reference
stations was vital in order to select a set of stable reference stations
to conduct the analysis for all stations in the monitoring network. The
results of stability analysis of two epoch’s data (4th and 5th Jan 2010)
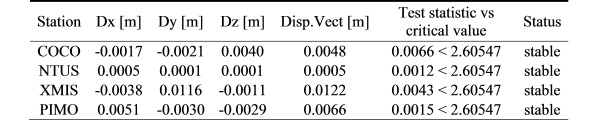
in Table 3 confirmed that all four reference stations were stable.
Table 3: Stability analysis of the
four reference stations using IWST
Subsequently, deformation analysis of all seven stations was carried
out via final S-transformations based on the stable reference points
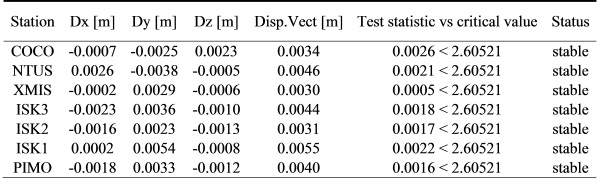
(Table 3). All seven stations were verified as stable (Table 4).
Consequently, the results obtained illustrate that the movement
experienced by the GPS CORS stations at cm level can be detected.
However, there was no significant movement as shown in Table 4.
Table 4: Stability of all monitoring
stations using final S-Transformation based on four stable reference
points
Next, GPS data (1st Jan 2010 – 31st Dec 2012) have been processed and
analysed continually using the devised technique. The epoch on 4th Jan
2010 and 1st Jan 2011 were selected as reference epoch for year 2010 and
year 2011 respectively that any epochs against it. The results of
stability analysis show all the stations are stable. The fluctuation of
CORS stations: ISK1, ISK2 and ISK3 can be revealed through plotting in
Northing, Easting and Up. Figure 12(a), 12(b), 12(c) show the variation
of ISK1, ISK2 and ISK3 in Easting, Northing and Up for year 2010.
Nevertheless, Figure 13(a), 13(b), 13(c) show the variation of ISK1,
ISK2 and ISK3 in Easting, Northing and Up for year 2011.

Figure 12(a): Variation of displacement vectors of ISK1 in
Easting, Northing and Up for year 2010. |
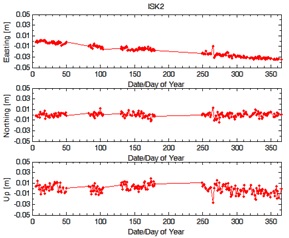
Figure 12(b): Variation of displacement vectors of ISK2 in
Easting, Northing and Up for year 2010. |
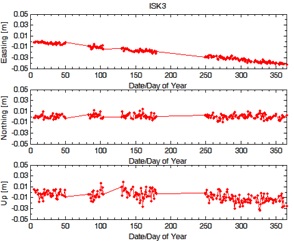
Figure 12(c): Variation of displacement vectors of ISK3 in
Easting, Northing and Up for year 2010. |
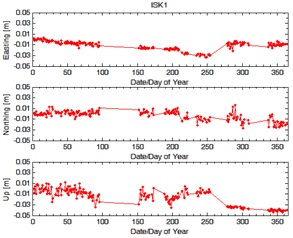
Figure 13(a): Variation of displacement vectors of ISK1 in
Easting, Northing and Up for year 2011. |

Figure 13(b): Variation of displacement vectors of ISK2 in
Easting, Northing and Up for year 2011. |
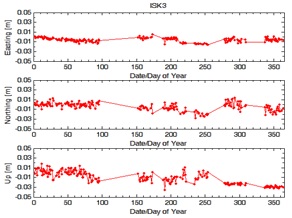
Figure 13(c): Variation of displacement vectors of ISK3 in
Easting, Northing and Up for year 2011. |
With respect to Figure 12(a), Figure 12(b) and Figure 12(c), Easting
component of ISK1, ISK2 and ISK3 were suspicious that undergo some
position changes throughout 2010. However, the displacements were
considered still under the safe condition and this three monitored
stations were deemed to be stable based on the computed deformation
analysis results. As an overall, the largest standard deviation of ISK1,
ISK2 and ISK3 reached 1.3 centimetres. It illustrates the obtained
results was promising enough in the context of consistency. Table 5
shows the data statistics of ISKANDARnet stations in year 2010.
Table 5: Statistical analysis of ISK1,
ISK2 and ISK3 for year 2010

Consequently, regarding to Figure 13(a), Figure 13(b) and Figure
13(c) deformation analysis of ISKANDARnet was interrupted due to some
rigorous on-site maintenance and software up-grading throughout the year
2011. GPS data was not available that caused gaps to occur all the way
in the plotting. In particular, largest standard deviation of ISK1, ISK2
and ISK3 achieved 1.5 centimetres. From Figure 13(a), Figure 13(b) and
Figure 13(c), Up component of three monitored stations was suddenly
slumped from day of year 280 until day of year 365. Further site
investigation was needed to ensure the location was free from threats.
Nevertheless, all monitored stations were deemed to be stable and no
significant displacement was detected in year 2011. Table 6 illustrates
the data statistics of ISK1, ISK2, and ISK3 for year 2011.
Table 6: Statistical analysis of ISK1,
ISK2 and ISK3 for year 2011

4. CONCLUSION
In this paper, the skeleton of continuous deformation analysis and
visualisation of GPS CORS has been illustrated. A combination of
strategy is devised to develop a compatible deformation detection
software system for CORS coordinate monitoring. To attain the millimeter
accuracy, some special processing strategies had been applied in the
Bernese GPS software. Three types of output files from Bernese software
were extracted for deformation detection and analysis. Consequently, a
windows-based software system for GPS deformation detection via IWST and
final S-transformation methods, called ConDAS, has been described. It
has been proven to have potential for providing high-quality stability
information for CORS network. The test results show the suitability of
this software system for practical applications. Furthermore, the
obtained results are very promising, indicating the suitability of
combining IWST and final S-transformation techniques for CORS coordinate
monitoring. The future works tend to improve the flexibility of this
software system in terms of data searching, loading and code embedding
towards a fully automated deformation monitoring system.
Acknowledgements
The authors would like to thank Department of Survey and Mapping
Malaysia (DSMM) for providing valuable MyRTKnet GPS data. The authors
are grateful to the following agencies for research funds: Ministry of
Science, Technology and Innovation (MOSTI) for Science Fund (Vot.
79350), Ministry of Higher Education (MOHE) for RUG (Vot.
Q.J130000.7127.02J69) and Land Surveyors Board (LJT) Malaysia. The
authors also grateful to GNSS & Geodynamics Research Group (FKSG,
Universiti Teknologi Malaysia) which provide the research facility for
data processing purposes.
REFERENCES
Aguilera, D.G., Lahoz, J.G. and Serrano, J.A.S., 2007. First
Experiences with The Deformation Analysis of A Large Dam Combining Laser
Scanning and High-accuracy Surveying. XXI International CIPA Symposium.
01-06 October. Athens, Greece.
Cai, J., Wang, J., Wu, J., Hu, C., Grafarend, E. and Chen, J., 2008.
“Horizontal deformation rate analysis based on multiepoch GPS
measurement in Shanghai.” J. Surv. Eng., 134(4), 132-137.
Caspary, W.F., 1988. Concept of Network and Deformation Analysis.
Monograph 11, School of Surveying, University of New South Wales,
Kensington, 183pp.
Chen, Y.Q., Chrzanowski, A. and Secord, J.M., 1990. A Strategy for
the Analysis of the Stability of Reference Points in Deformation
Surveys. CISM Journal ACSGC, 44(2): 141-149.
Chrzanowski, A., Caissy, M., Grodecki, J. and Secord, J., 1994.
Software Development and Training for Geometrical Deformation Analysis.
UNB Final Report. Contract No. 23244-2-4333/01-SQ.
Danisch, L., Chrzanowski, A., Bond, J. and Bazanowski, M., 2008.
Fusion of Geodetic and MEMS Sensors for IntegratedMonitoring and
Analysis of Deformation. Proceedings of the 4th IAG Symposium on Geodesy
for Geotechnical and Structural Engineering & 13th International (FIG)
Symposium on Deformation Measurement and Analysis. 12–15 May, Lisbon,
Portugal.
Haasdyk, J., Roberts, C. and Janssen, V., 2010. Automated Monitoring
of CORSnet-NSW using the Bernese Software. FIG Congress 2010, Sydney,
Australia, April 11-16.
Hu, Y.J., Zhang, K.F. and Liu, G.J., 2005. Deformation Monitoring and
Analysis using Regional GPS Permanent Tracking Station Networks. FIG
Working Week. Cairo, Egypt, April 16-21.
Hudnut, K. W., Bock, Y., Galetzka, J. E.,Webb, F. H. and Young, W.
H., 2001. The Southern California Integrated GPS Network (SCIGN).
Proceedings of the 10th FIG International Symposium on Deformation
Measurements. Orange, CA, USA, 19–22 March: 129–148.
Jager, R., Kalber, S. and Oswald, M., 2006. GNSS/GPS/LPS based Online
Control and Alarm System (GOCA) – Mathematical Models and Technical
Realisation of a System for Natural and
Geotechnical Deformation Monitoring and Analysis. Proceedings of the 3rd
IAG Symposium on Geodesy for Geotechnical and structural Engineering and
12th FIG Symposium on Deformation
Measurements. 22–24 May, Baden, Austria.
Janssen, V., 2002. GPS Volcano Deformation Monitoring. GPS Solutions.
6: 128-130, DOI 10.1007/s 10291-002-0020-8.
Jhonny, 2010. Post-Seismic Earthquake Deformation Monitoring in
Peninsular Malaysia using Global Positioning System. M. Sc. Thesis, pp.
58. Universiti Teknologi Malaysia.
Ji, K.H., and Herring, T.A., 2011. Transient Signal Detection using
GPS Measurements: Transient Inflation at Akutan Volcano, Alaska, During
Early 2008, Geophys. Res. Lett., 38, L06307, doi:10.1029/2011GL046904.
Jia, M.B., 2005. Crustal Deformation from the Sumatra-Andaman
Earthquake. AUSGEO news, issue 80.
Li, L. and Kuhlmann, H., 2010. “Deformation detection in the GPS
real-time series by the multiple kalman filters model”. J. Surv. Eng.,
136(4), 157-164.
Lim, M.C., Halim Setan and Rusli Othman, 2010. A Strategy for
Continuous Deformation Analysis using IWST and S-Transformation. World
Engineering Congress 2010, Kuching, Sarawak, Malaysia, 2-5 August.
Lim, M.C., Halim Setan and Rusli Othman, 2011. Continuous Deformation
Monitoring Using GPS And Robust Method: ISKANDARnet. Joint International
Symposium on Deformation Monitoring, Hong Kong, China, 2-4 November.
Lim, M.C., 2012. Deformation monitoring procedure and software system
using robust method and similarity transformation for ISKANDARnet. M.Sc.
thesis. Universiti Teknologi Malaysia.
Setan, H. and Singh, R., 2001. Deformation Analysis of a Geodetic
Monitoring Network. Geomatica. 55(3), 333-346.
Shariff, N.S.M., Musa, T.A., Ses, S., Omar, K., Rizos, C. and Lim,
S., 2009. ISKANDARnet: A Network-Based Real-Time Kinematic Positioning
System in ISKANDAR Malaysia for Research Platform. 10th South East Asian
Survey Congress (SEASC), Bali, Indonesia, August 4-7.
Vermeer, M., 2002. Review of The GPS Deformation Monitoring Studies
Commissioned by Posiva Oy on the Olkiluoto, Kivetty and Romuvaara sites,
1994-2000. STUK-YTO-TR 186. Helsinki.
Yu, M., Guo, H. and Zou, C.W., 2006. Application of Wavelet Analysis
to GPS Deformation Monitoring. IEEE Xplore. 0-7803-9454-2/06, 670-676.
BIOGRAPHICAL NOTES
Lim Meng Chan was a M.Sc. student at the Dept of Geomatic
Engineering, Faculty of Geoinformation and Real Estate, Universiti
Teknologi Malaysia (UTM). She holds B. Eng. (Hons) in Geomatic (2008)
and M.Sc. in Satellite Surveying (2013). Her master project focuses in
the area of GPS for continuous deformation monitoring under supervision
of Prof. Dr. Halim Setan and Mr. Rusli Othman.
Dr. Halim Setan is a professor at the Faculty of
Geoinformation and Real Estate, Universiti Teknologi Malaysia. He holds
B.Sc. (Hons.) in Surveying and Mapping Sciences from North East London
Polytechnic (England), M.Sc. in Geodetic Science from Ohio State
University (USA) and Ph.D from City University, London (England). His
current research interests focus on precise 3D measurement, deformation
monitoring, least squares estimation, laser scanning and 3D modelling.
CONTACTS
Prof. Dr. Halim Setan
Department of Geomatic Engineering,
Faculty of Geoinformation and Real Estate
Universiti Teknologi Malaysia (UTM)
81310 Johor Bharu
Johor
MALAYSIA
Tel. +607-5530908
Fax + 607-5566163
Email: halim@utm.my
Web site: -
 |