PORTABLE MOBILE MAPPING *)Cameron M. ELLUM and Dr. Naser EL-SHEIMY, CanadaKey words: Mobile Mapping, Close-Range Photogrammetry, Digital Compass, Low Cost. *) This paper is a updated version of - Ellum, C.M. and N. El.Sheimy. 2001. "A Mobile Mapping System for the Survey Community". Proceedings of The 3rd International Symposium on Mobile Mapping Technology (MMS 2001). Cairo, Egypt. January 3-5, 2001. On CD-ROM. AbstractIntroductionA low-cost backpack mobile mapping system (MMS) is being developed in the department of Geomatics Engineering at the University of Calgary (see the figure below). The goal of the system is to overcome the drawbacks of current mobile mapping systems - namely their high cost, large size, and complexity - that have restricted their widespread adoption in the survey industry. The development of such a system satisfies the demand for a mobile mapping system that can compete in both cost and user friendliness with current GPS and conventional terrestrial survey systems, while realizing the significant gains in efficiency available through the use an MMS. MethodologyThe system integrates a digital magnetic compass, dual-frequency GPSreceiver and consumer digital camera into a multi-sensor mapping system. The GPS pro-vides estimates of the camera's position at the exposure stations and the magnetic compass provides estimates of the camera's attitude. These exterior orientation estimates are then used as weighted parameter observations in a bundle adjustment. ResultsThe absolute and relative object space accuracies of the system are examined at different camera-to-object point distances using different numbers of images and different numbers of image point measurements. With three images at a 20m object-to-camera distance, absolute accuracies of under 25 cm are achieved. This is comparable to current single-frequency GPS data acquisition systems. The internal agreement of points surveyed using the system is under 10 cm. The effect of including additional observations is also examined. 1 INTRODUCTIONThere is an increasing demand in both government and private industry for geo-spatial data. Small and medium survey companies using traditional methods of data collection are filling much of this demand. However, these traditional techniques including GPS are costly and time consuming, and are not well suited for rapid collection of the large amounts of spatial data that GIS require. For the same reasons, the traditional techniques are not well suited for performing frequent updating. In an effort to overcome the draw- backs of traditional spatial data collection techniques, there has been much research into the creation of mobile mapping systems (MMS). MMS combine navigation sensors such as GPS and INS with mapping sensors such as CCD Cameras or Pushbroom Scanners and are successful in overcoming many of the disadvantages of traditional surveying techniques. Detailed examinations of MMS can be found in Li (1997) or El-Sheimy and Ellum (2001) and examples of their implementation can be found in Bossler and Novak (1993), El-Sheimy (1996), Toth and Grejner-Brzezinska (1998) or Mostafa and Schwarz (1999). All of these publications agree that the advantages of MMS are both varied and numerous; however, the key benefits are:
Despite these advantages, current mobile mapping systems have not gained widespread acceptance in the survey community. The reluctance to adopt MMS technology stems primarily from two sources cost and complexity. Until now, MMS have predominantly been implemented on vans or aeroplanes. These systems typically integrate dual- frequency GPS receivers and navigation grade Inertial Measurement Units (IMUs) with a variety of mapping sensors. Because of these components, these systems are very ac- curate; however, they are also very expensive and very complex. Only large companies and government organisations have both the expertise and resources which are required to operate the systems, and consequently, the smaller survey and mapping firms continue to use traditional survey techniques for projects requiring GIS data collection. The goal of the development of a backpack mobile mapping system is to overcome the drawbacks of current mobile mapping systems that are limiting their acceptance in the survey community. The backpack MMS will compete in accuracy with current methods of GIS data collection, but it will also offer the advantages in efficiency and flexibility that only an MMS can provide. Applications of a backpack mobile mapping system are numerous. They include pipeline right-of-way mapping, urban GIS data acquisition, high- way inventory, facility mapping, architectural reconstruction and small-scale topographic mapping. This paper provides a brief background on the navigation and mapping sensors selected for the MMS. It then examines the accuracy of the navigation sensors, and concludes with the results of tests using conducted with the system. 2 NAVIGATION AND MAPPING SENSORSAs detailed above, all mobile mapping systems are a combination of different navigation and mapping sensors. For the backpack MMS, the sensors used are a digital compass, a GPS receiver, and a consumer digital camera. 2.1 Digital CompassTo determine orientation, the Backpack MMS uses a Leica Digital Magnetic Compass (DMC). The DMC combines three micro-electromechanical (MEMs) based accelerometers and three magnetic field sensors. The accelerometers sense the direction of earth's gravity vector; from this, the roll and pitch angles can be easily calculated. Similarly, the azimuth is determined from the components of earth's magnetic field sensed by the magnetic field sensors. Because the earth's magnetic field is the reference, the azimuth angles from the DMC are referenced to magnetic north. Therefore, they must be corrected for magnetic declination if they are to refer to true north. Fortunately, there are freely available global models of earth's magnetic field that are considered accurate to better than 1º (GSC, 2000). More accurate regional and local models are also available. The specifications of the DMC are shown in Table 1, and the DMC itself is shown in Figure 1.
Figure 1: Leica Digital Magnetic Compass (DMC)
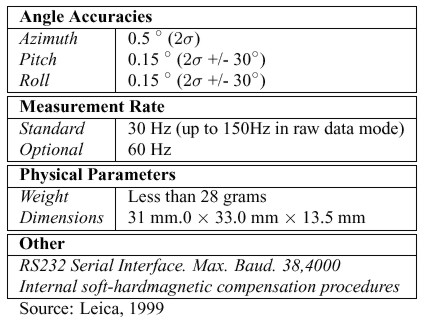
Table 1: Leica DMC-SX Specifications The accuracy of the azimuth angles reported by digital compasses depends heavily on the degree to which the local magnetic field is being disturbed. Disturbances in the magnetic field can be divided into two categories: softmagnetic, which are caused by nearby magnetic materials, and hardmagnetic, which result from nearby electric fields and magnets. If the sources of these disturbances are fixed relative to the magnetic sensors such as the camera and GPS antenna on the backpack MMS then their effect can be removed through calibration. The DMC implements several internal calibration routines that per- form both softmagnetic and hardmagnetic calibrations. For a review of hardmagnetic disturbances, softmagnetic disturbances, and a general introduction to digital compasses, see Caruso (2000). As a final note, disturbances that are not fixed can obviously not be compensated for, and must therefore be avoided. 2.2 GPSGPS has been the primary motivator for the development of mobile mapping systems of any type (Li, 1997). Thus, its inclusion in the backpack MMS is obvious. Indeed, no other positioning technology offers anywhere near the same accuracy and flexibility at the same cost and small size. The GPS receiver currently being used in the backpack MMS is a Novatel dual-frequency RT2. Waypoint Consulting's Grafnav TM Kinematic GPS processing software is being used to process the GPS measurements. 2.3 Consumer Digital CameraThe digital camera currently being used in the backpack MMS is the Kodak DC260. Consumer digital cameras are ideal for inclusion in portable mobile mapping systems because of their large colour image format, low cost, and large internal memory. The internal memory of the camera is particularly valuable because it negates the requirement to transfer the images to a logging computer. The Kodak DC260 is particularly well suited for close range photogrammetry because of its ability to fix its focus at infinity thus avoiding the changes in interior orientation that result because of changes in focus. 3 SYSTEM CONFIGURATIONThe development of the backpack MMS is still underway; however, Figure 2 shows the anticipated arrangement of the various sensors. In this arrangement, the DMC makes continuous measurements of roll, pitch, and yaw. Admittedly, for this application continuous measurements of the attitude angles are not required, but making continuous measurements simplifies the system because it removes the requirement to communicate with the DMC while surveying. In other words, once the DMC is started, the logging software no longer has to interact with it. The measurements from the DMC are sent to the GPS receiver which time-tags them and forwards them to the logging computer. The GPS receiver is also responsible for marking the times of exposure. An exposure-mark is generated every time a signal from the camera's external flash is received by the receiver. It is important to note the camera itself is responsible for storing the images and that the GPS receiver only marks the times of image captures. This arrangement greatly reduces the volume of data that must be sent to the GPS receiver and, in turn, the logging computer.
Figure 2: Backpack MMS System Configuration The GPS is the "core" of the arrangement shown above. This arrangement differs from standard MMS where the logging computer is responsible for handling the data streams from the various sensors. However, using the GPS receiver as the data handler has two significant advantages. First, it simplifies time-tagging of the various data streams. Sec- ond, it reduces the communication requirements for the logging computer i.e, only one communications port is required. 4. MATHEMATICAL BACKGROUNDThe basis of the collinearity equations used in a photogrammetric
bundle adjustment is a seven-parameter conformal transformation that
relates image measurements of a point
In Equation (1), In the backpack MMS, both the position of the camera perspective
centre and the rotation matrix between the camera frame and the
mapping frame are measured - albeit indirectly. In reality, the GPS
provides the position of the antenna phase center
The DMC provides the roll, pitch, and yaw angles that relate the
mapping co-ordinate frame to DMC co-ordinate frame. These angles are
used to form the rotation matrix
Using Equation (3), it is possible to determine an analytical
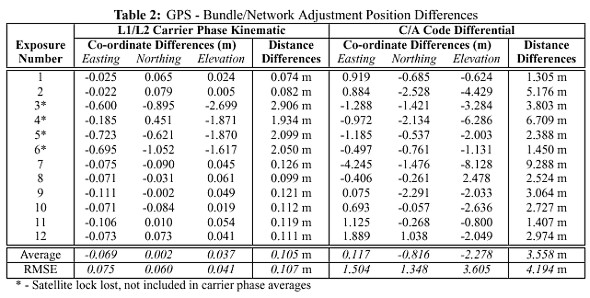
relation between the roll, pitch, & yaw angles, and the Once the estimates of camera position and orientation are determined, then they can be included in a bundle adjustment as weighted parameter estimates (Mikhail, 1976). Obviously, if there is no control in the images, then apriori precision estimates of the parameters are required to prevent rank deficiencies in the normal matrix. The physical interpretation of the parameter estimates is that the GPS positions are "tying-down" the scale, translation, and depending on their number one or more of the rotations of the datum. Similarly, the DMC angles fix the rotations of the datum. The mathematical interpretation of the parameter estimates is that they act as stochastic constraints on the definition of the datum (Cooper and Robson, 1996). With parameter estimates for both the positions (from GPS) and the attitude angles (from the DMC), the backpack MMS can operate with as few as two images. Indeed, with two images - both with GPS positions and DMC angles - there is actually redundant information for all of the datum parameters except scale. Operationally, however, it is advantageous to use at least three images, as there will then be redundant information for all datum parameters. Providing that points are imaged in all three images, there will also be redundant information for the object space points as well. 5 RESULTSThe primary goal of the backpack MMS testing was to determine the achievable mapping accuracies of the integrated system. However, prior to this test being performed it was first necessary to investigate the real-world performance of the navigation sensors. Both tests necessitated a suitable target field that simulated a "typical" urban environment in which the backpack MMS would be expected to operate. Therefore, a target field was established that had nearby vertical structures, pavement, and foliage in short, some- what of a "worse-case" environment for GPS. It also had nearby metal buildings and light standards that could influence the azimuth reported by the DMC. The target field was initially surveyed and adjusted using GPS baselines, EDM distances, and horizontal & vertical angles. To further increase the accuracy of the surveyed points, and to most ac- curately determine the exterior orientations of the test images, the measurements from all the images used in the tests were also included in a combined photogrammetric/terrestrial adjustment. Additionally, the interior orientation and lens distortion parameters of the camera were calibrated simultaneously, although results from a previous calibration were included as weighted parameters. The combined network had a redundancy of over 1500, and the reported standard deviations for the object space co-ordinates of both the target points and exposure station positions were under a millimetre. The attitudes of the exposure stations had standard deviations that were largely less than one arc-minute. The positions and orientations calculated in the combined photogrammetric/terrestrial adjustment were treated as the "true" quantities in all the comparisons in the following sections. The residual error that remains was neglected, as its relative magnitude was below the centimetre level that the results were compared at. The initial terrestrial network adjustment, the combined adjustment, and the individual photogrammetric adjustments done for the tests were all performed using the bundle adjustment package described in section 6. The images for the tests were taken at object to camera distances of approximately 20m and 40m hereafter referred to as the "near" and "far" images respectively. Initially, two images were captured at each of six image stations - 3 near and 3 far. In the description of the tests, images 1 through 6 are the near images and images 7 through 12 are the far images. In all cases, the azimuths from the DMC have first been corrected for magnetic declination using the Geological Survey of Canada's Magnetic Information Retrieval Program (MIRP) (GSC, 2000). 5.1 Navigation Sensor PerformanceTable 2 shows the agreement between the measured GPS positions and the camera positions determined from the combined photogrammetric/terrestrial adjustment. The results show that the test environment was indeed sub-optimal, as the results are significantly worse than expected especially considering that the master to remote separation never exceeded 150m and the number of satellites never fell below 6. It is believed that multi-path off the nearby buildings is the cause of the poor accuracies. Carrier phase results for images 4 through 6 are significantly worse than the others because of a loss of satellite lock after the second image; thus, these differences were not included in the statistics. This loss of lock illustrates that for urban environments, at least Real-Time Kinematic (RTK) GPS may be more of a necessity than a luxury. This is because despite the extreme care taken during these tests to avoid losing lock, loss of lock still occurred. Such an occurrence would likely befall any user in a similar environment, and only with RTK could the approximate accuracies be reliably maintained. It is also worth noting that in the environment that the test was performed a code differential solution is clearly far too inadequate for even the crudest mapping applications. This does not, however, completely preclude its use in the backpack MMS, as additional testing in other environments is required.
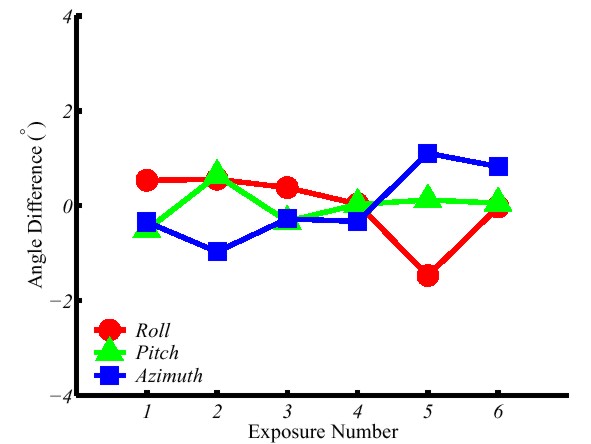
The differences between the attitude angles measured by the DMC and the true attitude angles are shown in Figure 3 and Table 3. For this test, the DMC attitude angles were collected at approximately 10 Hz. At this sampling frequency, the measurements are moderately noisy particularly the azimuth, which can vary over several degrees. Therefore, to remove some of this noise one-second averages of the DMC data were used. This improved the agreement of the roll and pitch angles by approximately 8 arc-minutes, and of the azimuth angles by over half a degree. It is felt that this is a reasonable time period, as the backpack MMS must be held steady for at least this period in order to capture the image. The results in Table 3 are the differences after the mean has been removed from the differences between the DMC angles and the true angles. This was done because time did not permit a full calibration of the integrated system, and the average angular differences were used as an estimate of the misalignment between the camera axes and the DMC axes. Of course, simply removing the mean will result in an overly-optimistic estimate of the angular errors particularly for the azimuth as it will also compensate for both deficiencies in the magnetic declination model and local variations of the magnetic field (although the mean of the azimuth differences was the smallest of the three angles prior to removal). Finally, it should be noted that the DMC was not calibrated for either hard or softmagnetic disturbances, and the azimuth angle results in Table 3 would certainly be improved by either such calibration. The agreement between the measured angles and the true angles in Table 3 is generally good. However, there is a notable and surprising decline in accuracy for the azimuths of the final four exposure stations. A possible explanation was the proximity of a nearby electric light standard and metal building, but it was felt that these objects could not disturb the magnetic field to the extent visible in Table 3. Thus, the results were checked by capturing additional images at approximately the same positions as the final six images from the first data set (i.e., the far images). For this second set of images the internal data integration time of the DMC was changed so that measurements were collected at 1 Hz. Unfortunately, GPS was not available for these images, and because the DMC was remounted, new angular difference averages were calculated and again used in lieu of a rigorous calibration.
Figure 3. DMC/Combined Adjustment Angle Differences
Table 3. DMC/Combined Adjustment Angle Differences The azimuth differences for the new photos shown in Figure 4 and Table 4 are significantly smaller than the differences for the previous photographs taken at the exposure stations. The cause of the azimuth errors in the first set of images is unknown; however, one possibility may be that the power cable for the camera was allowed to come too close to the DMC.
Figure 4. DMC/Combined Adjustment Angle Differences - Second Set of Far Images
Table 4. DMC/Combined Adjustment Angle Differences - Second Set of Far Images 5.2 Mapping AccuracyAs outlined in section 4, the object space co-ordinates from the backpack MMS are determined using a bundle adjustment with the image point measurements and positions and orientations of the exposure stations measured by the GPS and DMC. Unfortunately, the loss of satellite lock discussed in section 5.1 meant that it was not possible to use the carrier phase GPS positions for the final four exposures of the near exposure stations. Therefore, the positions from the combined photogrammetric/terrestrial adjustment were used instead. To simulate the effect of positioning errors, the co-ordinate errors from the equivalent far stations were added to the exposure station positions. Also, the erroneous DMC angles for the initial far images meant that no adjustment would converge for these images. Thus, the second set of far images with the correct DMC angles were used. Because GPS was not used for these images, position errors were simulated by adding the co-ordinate errors from the first set of far stations to the `true' exposure stations. The object space accuracies when the near images were used are shown in Table 5. For the first two tests in the table the six close images were divided into two sets of three images set `A' was composed of images 1, 3, and 5, while set `B' was composed of images 2, 4, and 6. Not surprisingly, the most obvious trend in Table 5 is an increase in absolute object space accuracy as the number of image points included in the bundle adjustment increases. However, even with as few as five points, accuracies are comparable with typical L1 carrier phase GPS accuracies. This accuracy was something of a benchmark, as such single frequency receivers are widely used for GIS data collection. Of course, the backpack MMS is able to achieve this accuracy with a much greater data collection efficiency.
Unfortunately, the encouraging results for the near images are somewhat offset by disappointing results for the far images. These results, shown in Table 6, indicate absolute object space accuracies at the metre level. This degradation in performance for the far images has two sources:
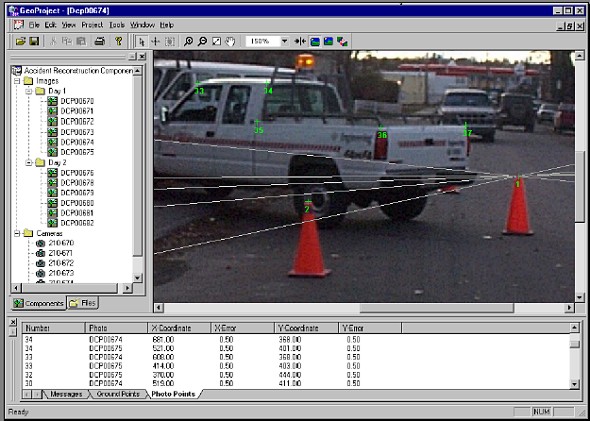
The potential existence of poor image measurements highlights an additional problem that of blunder detection. Obviously, in photogrammetric networks as redundancy decreases this becomes progressively more difficult. For some users of the backpack MMS, low redundancy will be the norm and not the exception. In these cases the graphical image measurement software can help in both the prevention and detection of errors. For example, the display of epipolar lines will help prevent blunders during image point mensuration, while the back-projection of the adjusted object-space points will help in the detection of any poor measurements.
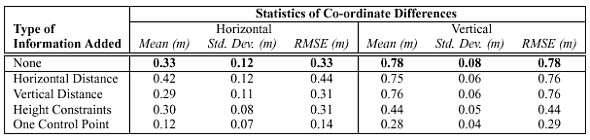
Table 6. Results (Approximate Camera to Object Point Distance = 40 m) For both the near and the far images, it can be observed that the mean of the differences is nearly as large as the RMS error. This indicates that the relative accuracy of the object points is much better than their absolute accuracy. This is confirmed by the standard deviations of the co-ordinate errors, which indicate that the internal agreement of the object space co-ordinates is at approximately 5 cm for the near images and 10 cm for the far images. It is acknowledge that absolute accuracies are of primary importance for most mapping and GIS applications. However, relative accuracies still have importance in cadastral and engineering surveys - examples include small-scale facilities mapping and surveys for earthwork volume computations. 5.3 Effect of Additional Observations and ConstraintsThe objective of the backpack MMS is to produce co-ordinates without any external measurements i.e., with no control points. However, this does not preclude the use of additional information that may available in the images such as objects of known dimension or a known geometry between points. The former information in the form of distance constraints should improve the scale of the photogrammetric networks measured from the backpack MMS's images. Similarly, the latter information in the form of vertical line constraints or zero-height constraints should help with the orientation of the net- works. Unfortunately, the effects of including such information are not always positive. Indeed, for the tests in Table 7 the additional information was equally as likely to degrade the solution as it was to improve it. This surprising result which was confirmed in other tests requires further investigation.
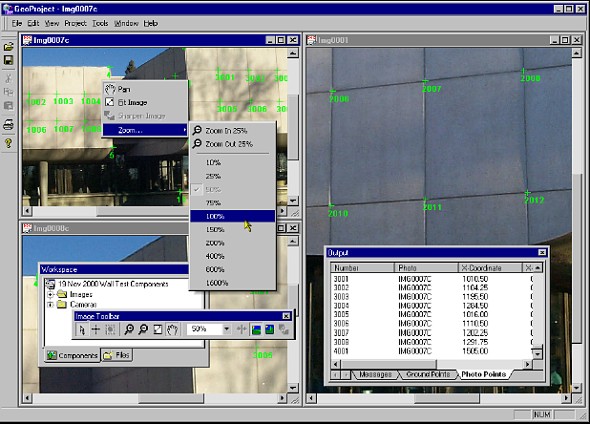
Table 7. Effect of Including Control or Network Observations (3 images, 10 image points, far images) Table 7 also demonstrates the obvious improvement in both absolute and relative accuracy that results from including a control point in the adjustment. One potential mode of operation of the backpack MMS is to have it mounted on a survey stick. In this case, using the GPS the MMS itself could be used to establish control points in a region. These points, in turn, could then be used in the adjustment to improve absolute accuracy. In other words, a user would occupy points with the survey stick mounted MMS, and then include those GPS points in the adjustment providing, of course, that the points appear in the images. 6 SOFTWARE FOR CLOSE-RANGE PHOTOGRAMMETRYFor the backpack MMS to achieve its goal of bringing mobile mapping into a wider market, user-friendly software is essential. Consequently, such software is being developed concurrently with the development of the backpack MMS. When completed, the software package will be capable of processing the navigation data, manipulating the images, calculating the 3-D mapping co-ordinates of features visible in the images, and exporting all information to a database. Conceptually, the software is the same as similar "integrated" close-range photogrammetric packages such as that described in and Fraser and Edmund- son (2000). The goal of the software is also the same as that of Fraser and Edmundson - to bring rigorous photogrammetric tools to less specialised users. To that end, development of the software has proceeded along two lines. The first is algorithmic development to implement photogrammetric principles - i.e., a self-calibrating bundle adjustment. For increased flexibility, the bundle adjustment has also been designed to incorporate terrestrial network observations - either separately, or in combination with photogrammetric observations. The second line of development is the implementation of a stable and user- friendly graphical interface. Screen shots of the latter are shown in Figure 5.
(a) Multiple Epipolar Lines
(b) Advanced GUI Figure 5. Close-Range Photogrammetric Software 7 CONCLUSIONS AND FUTURE WORKResults presented in this paper have shown that a backpack MMS constructed from off- the-shelf hardware can have absolute object space accuracies comparable to current GIS data acquisition techniques. Furthermore, the internal agreement or relative accuracies of the object space points is even better. Using three images at a 20m object-to-camera distance, absolute accuracies of under 25 cm are achieved, and the internal agreement of points surveyed using the system is under 10 cm. With a more rigorous calibration of the both the DMC and of the integrated system, even better results are likely. 8 ACKNOWLEDGMENTSFunding and support for this research is provided by Premier GPS. The authors are also grateful to Waypoint Consulting for making their Grafnav TM GPS processing software available, and to Quentin Ladetto, Jos van Seeters and Leica Technologies Inc. for their help with the DMC. Finally, Dr. Mike Chapman and Dr. Derek Lichti are thanked for providing their FEMBUN self-calibrating bundle adjustment software that was used for comparison purposes with the author's own software. REFERENCESBossler, J.D. and K. Novak. 1993. "Mobile Mapping Systems: New Tools for the Fast Collection of GIS Information". In Proceedings of GIS 93 . Ottawa, Canada. March 23-35. pp. 306-315. Caruso, M.J. 2000. "Applications of Magnetic Sensors for Low Cost Compass Systems". In Proceedings of IEEE Positioning, Location, and Navigation Symposium (PLANS) 2000 . San Diego. March 13-16. pp. 177-184. Cooper, M.A.R. and S. Robson. 1996. "Theory of Close Range Photogrammetry". In Close Range Photogrammetry and Machine Vision . ed. K.B. Atkinson. J.W. Arrow- smith. Bristol. pp. 9-50. El-Sheimy, N. 1996. "A Mobile Multi-Sensor System for GIS Applications in Urban Centers". International Archives of Photogrammetry and Remote Sensing . Vol. XXXI. Part B. Proceedings of the XVIII ISPRS Congress. Vienna. pp. 95-100. Ellum C.M. and N. El-Sheimy. 2001. "Land-Based Integrated Systems for Mapping and GIS Applications". To be published in proceedings of Italy - Canada 2001 Workshop on 3D Digital Imaging and Modelling . Padova, Italy. April 3-4. Fraser, C.S. and K.L. Edmundson. 2000. "Design and Implementation of a Computa- tional Processing System for Off-Line Digital Close-Range Photogrammetry". IS- PRS Journal of Photogrammetry and Remote Sensing . Vol. 55. pp. 94-104. Geological Survey of Canada (GSC). 2000. "Magnetic Declination". Website. URL: http://www.geolab.emr.ca/ geomag/e magdec.html. GSC National Geomagnetism Program. Site Accessed 31 Oct. 2000. Li, R. 1997. "Mobile Mapping: An Emerging Technology for Spatial Data Acquisition". Photogrammetric Engineering and Remote Sensing (PE&RS) . Vol. 63. No. 9. pp. 1085-1092 Leica. 1999. DMC-SX Performance Specifications. Leica Product Literature. Mikhail, E.M. 1976. Observations and Least Squares . Harper and Row. New York. Mostafa, M.M.R, and K.P. Schwarz. 1999. "An Autonomous Multi-Sensor System for Airborne Digital Image Capture and Georeferencing". In Proceedings of ASPRS Annual Convention . Portland, Oregon. May 17-21. pp. 976-987. Toth, C. and D.A. Grejner-Brzezinska. 1998. "Performance Analysis of the Airborne Integrated Mapping System (AIMS T M )". International Archives of Photogrammetry and Remote Sensing . Vol. XXXII. Proceedings of ISPRS Commission II Symposium. Cambridge, U.K. July 13-17. pp. 320-326. BIOGRAPHICAL NOTEDr. Naser El-Sheimy - is an Assistant Professor at the Department of Geomatics Engineering of the University of Calgary. He holds a B.Sc. and M.Sc. from Egypt, two post-graduate Diplomas in Photogrammetry and Remote Sensing from ITC, the Netherlands, and a Ph.D. from the University of Calgary. His area of expertise is the integration of GPS/INS/imaging sensors for mapping and GIS applications with special emphasis on the use of multi-sensor in Mobile Mapping Systems. He is now the chairman of the special study group for Mobile Multi-Sensor Systems of the International Association of Geodesy and the chairman of The International Federation of Surveyors (FIG) working group C5.3 on "kinematic and Integrated Positioning Systems" Cameron Ellum is currently completing his M.Sc. at the department of Geomatics Engineering at the University of Calgary. His research is in the area of mobile mapping systems and multi-sensor integration. Previous work experience has included oil-field surveying in Alberta and an internship in the survey and mapping department of a large multi-national pipeline corporation. CONTACTDr. Naser El-Sheimy and Cameron M. Ellum 19 April 2001 This page is maintained by the FIG Office. Last revised on 15-03-16. |